



A classe hem treballat els polígons inscrits en una circumferència. Hem fet:
1. El quadrat.
2. El triangle.
3. El pentàgon,
4. L'hexàgon.
5. L'octògon
Arquimedes va trobar el que va passar a ser anomenat mètode clàssic per estimar π. Trobar la longitud L d'una circumferència directament a partir del seu diàmetre potser no es pot resoldre, però Arquimedes va proposar inscriure i circumscriure un polígon a la circumferència, dels quals si que en podem calcular fàcilment el perímetre (Pi,Pc), per tal de trobar una aproximació, ja que 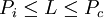 .
.
Comencem, per exemple, amb un hexàgon. Podem calcular els perímetres de l'hexàgon inscrit i circumscrit a la circumferència, de la qual en coneixem el diàmetre. Un cop calculats, dividint pel diàmetre de la circumferència, tenim una primera aproximació a π:  . No és una aproximació gaire precisa, però ara es poden duplicar els costats del polígon inscrit i circumscrit, i calcular-ne fàcilment el perímetre! D'aquesta manera, repetint el procés es poden trobar aproximacions cada cop més precises per a π.
. No és una aproximació gaire precisa, però ara es poden duplicar els costats del polígon inscrit i circumscrit, i calcular-ne fàcilment el perímetre! D'aquesta manera, repetint el procés es poden trobar aproximacions cada cop més precises per a π.
Arquimedes va arribar a calcular-ho amb polígons de 96 costats, trobant una aproximació per a π de:  , d'on
, d'on  .
.
De fet, per trobar el perímetre del polígon circumscrit, C2n, i el de l'inscrit, i2n, en funció dels perímetres ja calculats de n costats, es pot fer mitjançant:


(Aquesta informació ha estat extreta de: http://ca.wikipedia.org/wiki/Hist%C3%B2ria_del_nombre_%CF%80)
